Packages and setup
We’ll use RR-BLUP for kinship-based genomic prediction. Under the assumption that every locus in the genome contributes equally to variance in the phenotype, the genotype matrix can be reduced to a square kinship matrix, which considerably reduces computational time. There are other methods that assume variance is different from locus to locus, which you might look into if you are doing genomic prediction in your own work.
If you don’t already have rrBLUP, install it:
install.packages("rrBLUP")
Then load it into your R environment:
library(rrBLUP)
So that my results are identical you yours, I am setting a random seed.
set.seed(050919)
Dataset
We will use the Miscanthus sacchariflorus dataset from the polyRAD tutorial, with 268 individuals and 5097 loci. In that tutorial we formatted posterior mean genotypes for rrBLUP.
load("Msa_tetraploids_Chr05_rrb.RData")
str(rrb_geno)
## num [1:268, 1:13168] -0.998 -0.488 -0.955 -0.95 -1 ...
## - attr(*, "dimnames")=List of 2
## ..$ : chr [1:268] "PMS-458" "KMS-widespread" "UI10-00117" "UI11-00005" ...
## ..$ : chr [1:13168] "S05_51928_TTA" "S05_51928_TCC" "S05_51928_ATC" "S05_81981_GG" ...
Because many loci had multiple alleles, we have data for 13,168 alleles, treating each allele as though it were a biallelic marker. The common allele was omitted for each locus. The data are scaled so that -1 indicates zero copies of the allele, and 1 indicates four copies.
rrb_geno[1:20,1:4]
## S05_51928_TTA S05_51928_TCC S05_51928_ATC S05_81981_GG
## PMS-458 -0.9977491 -0.9995375 -0.48643582 -0.89401482
## KMS-widespread -0.4882062 -0.9999996 -0.45221813 -0.22711990
## UI10-00117 -0.9552068 -0.9828333 -0.94066904 -0.08923438
## UI11-00005 -0.9498768 -0.9999478 0.01539608 -0.20081827
## UI11-00027 -0.9998837 -0.9371307 -0.86813735 -0.38057506
## IGR-2011-005 -0.9999818 -0.9999818 -0.97271681 -0.20729142
## PMS-457 -0.9991914 -0.9998661 -0.49537841 -0.95534980
## JY186 -0.8589097 -0.9990854 -0.59061653 0.08264042
## JY192 -0.9352424 -0.9994995 -0.81117141 -0.21351398
## JY182 -0.8445864 -0.9998000 -0.58176430 -0.52157289
## JY009 -0.9526232 -0.9539069 -0.87427743 -0.31316810
## KMS408 -0.9550198 -0.9999378 -0.86064424 -0.27379817
## JY008 -0.8935263 -0.8574864 -0.68295009 -0.29383659
## JY127 -0.9483170 -0.9926090 -0.83100771 -0.32570147
## KMS417 -0.8483431 -0.9998000 -0.69749405 -0.48547984
## JY006 -0.9277114 -0.9127454 -0.82336644 -0.30865466
## JY129 -0.9191291 -0.9737688 -0.76240997 0.21654157
## JM2014-S-3 -0.8604225 -0.8186464 -0.82442143 -0.06291690
## JM2014-M-3 -0.8320151 -0.9455931 -0.83181124 -0.19655112
## JY183 -0.4502993 -0.9999074 -0.78606101 -0.25377510
For example, here we can see that “KMS-widespread” and “JY183” each likely have one copy of the TTA allele at S05_51928. “UI11-00005” likely has two copies of the ATC allele at this same locus.
The phenotype data is in a CSV:
pheno <- read.csv("Msa_tetraploids_pheno.csv", stringsAsFactors = FALSE)
head(pheno)
## Taxa Stem_diameter
## 1 PMS-458 2.127315
## 2 KMS-widespread 1.780867
## 3 UI10-00117 2.282351
## 4 UI11-00005 2.197177
## 5 UI11-00027 2.880700
## 6 IGR-2011-005 2.507009
We will subset to just taxa that have data, leaving 230 taxa:
pheno <- pheno[!is.na(pheno$Stem_diameter),]
str(pheno)
## 'data.frame': 230 obs. of 2 variables:
## $ Taxa : chr "PMS-458" "KMS-widespread" "UI10-00117" "UI11-00005" ...
## $ Stem_diameter: num 2.13 1.78 2.28 2.2 2.88 ...
all(pheno$Taxa %in% rownames(rrb_geno))
## [1] TRUE
rrb_geno <- rrb_geno[pheno$Taxa,]
str(rrb_geno)
## num [1:230, 1:13168] -0.998 -0.488 -0.955 -0.95 -1 ...
## - attr(*, "dimnames")=List of 2
## ..$ : chr [1:230] "PMS-458" "KMS-widespread" "UI10-00117" "UI11-00005" ...
## ..$ : chr [1:13168] "S05_51928_TTA" "S05_51928_TCC" "S05_51928_ATC" "S05_81981_GG" ...
Estimating the relationship matrix
From these genotypes, we will use rrBLUP to calculate the realized additive relationship matrix. This is accomplished with the A.mat function. No imputation is necessary since polyRAD already used genotype priors to impute any genotypes with zero reads.
Msa_A <- A.mat(rrb_geno)
heatmap(Msa_A)
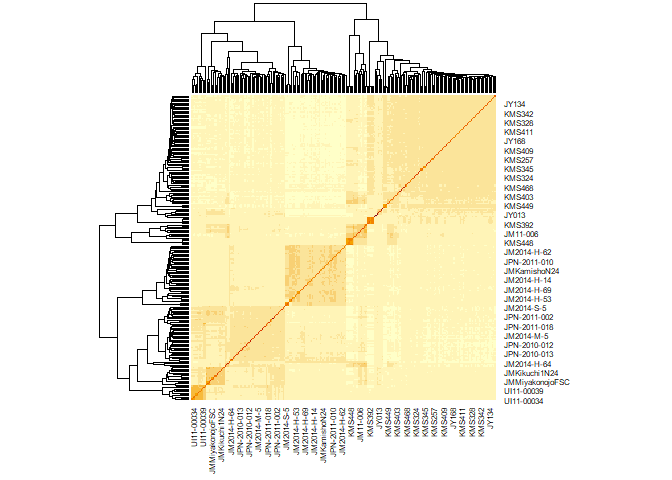
The clustering makes sense here. The biggest split is between Japan (lower left) and mainland Asia (upper right), and Japan is divided into north and south.
Setting up functions for cross-validation
To test the accuracy of our genomic prediction, we will perform five-fold cross validation. To do this, we will divide our set of individuals into five groups at random. We will then perform genomic prediction five times, each time with one of the groups being the prediction set (phenotypes unknown) and the other four being the training set (phenotypes known). We will see how accurately our predicted phenotypes match the real ones. We will repeat that whole process 100 times.
Below is a function to make the random groups.
# Function to divide a set of individuals randomly into a set of gruops
# for X-fold cross-validation.
# nind is the total number of individuals.
# ngrp is the number of groups desired.
# The output is a list of vectors, with each vector giving the indices of
# individuals in a group.
GenerateGroups <- function(nind, ngrp){
outlist <- vector("list", ngrp) # to contain output
scramble <- sample(nind) # random order for individuals
nPerGrp <- rep(nind %/% ngrp, ngrp) # number of individuals in each group
nExtra <- nind %% ngrp # number of individuals left over
# increase size of some groups by 1 to get to total needed
nPerGrp <- nPerGrp + rep(c(0, 1), times = c(ngrp - nExtra, nExtra))
# fill in vectors
for(i in 1:ngrp){
if(i == 1){
firstind <- 1
} else {
firstind <- sum(nPerGrp[1:(i - 1)]) + 1
}
lastind <- firstind + nPerGrp[i] - 1
outlist[[i]] <- sort(scramble[firstind:lastind])
}
return(outlist)
}
# Test the function
testgrp <- GenerateGroups(102, 5)
testgrp
## [[1]]
## [1] 2 4 14 16 17 21 28 29 32 37 39 45 48 56 59 65 89 92 93 97
##
## [[2]]
## [1] 5 6 9 15 18 23 33 38 47 53 54 64 66 67 69 73 84 90 95 98
##
## [[3]]
## [1] 8 11 12 26 30 40 41 44 49 50 51 57 61 62 79 81 82
## [18] 83 94 102
##
## [[4]]
## [1] 1 3 7 13 19 24 27 31 34 35 36 42 43 46 68 70 76 78 85 86 96
##
## [[5]]
## [1] 10 20 22 25 52 55 58 60 63 71 72 74 75 77 80 87 88
## [18] 91 99 100 101
sapply(testgrp, length)
## [1] 20 20 20 21 21
If were were going to do genomic prediction using the entire dataset as the training set, we would do it using kin.blup like this:
mypred <- kin.blup(data = pheno, geno = "Taxa", pheno = "Stem_diameter",
K = Msa_A)
plot(pheno$Stem_diameter, mypred$g)
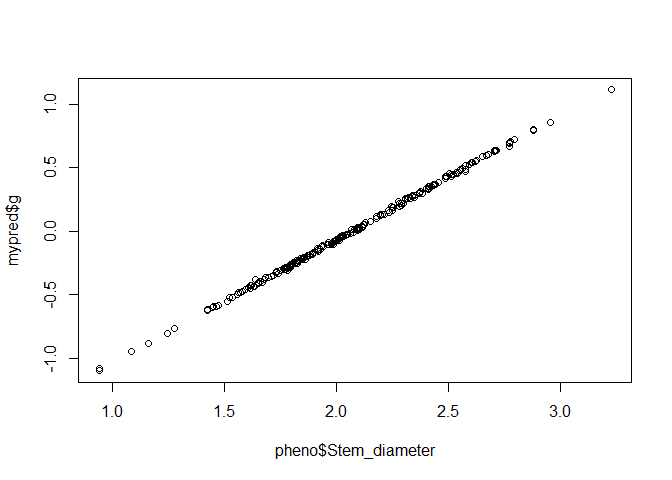
For cross-validation however, we want to mask some genotypes with NA.
phenoMasked <- pheno
toMask <- sample(230, 230/5)
toMask
## [1] 101 43 155 41 102 70 129 189 77 151 131 35 83 182 158 207 117
## [18] 25 213 196 194 54 127 219 135 208 81 211 86 228 13 191 123 50
## [35] 143 112 181 169 84 122 197 24 8 216 205 3
phenoMasked$Stem_diameter[toMask] <- NA
mypred <- kin.blup(data = phenoMasked,
geno = "Taxa", pheno = "Stem_diameter",
K = Msa_A)
plot(pheno$Stem_diameter[toMask], mypred$g[toMask])
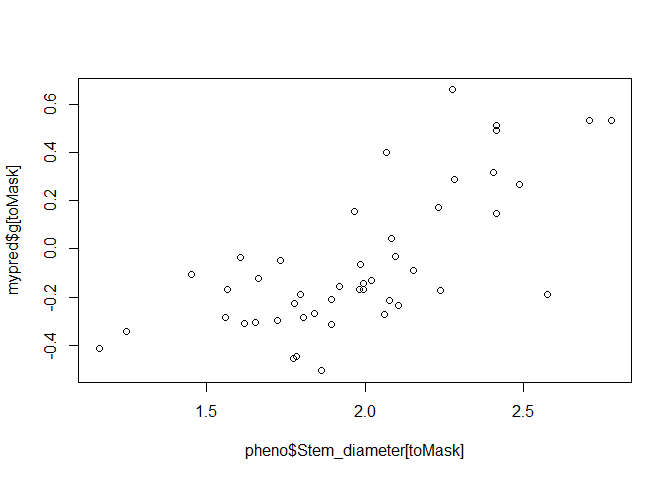
This gives a much more accurate depiction of how well genomic prediction will work.
We can put that together into a function to get predicted values for all taxa.
PredictPheno <- function(pheno, K, fold = 5){
ntaxa <- nrow(pheno) # number of taxa
predval <- numeric(ntaxa) # to hold predicted values
names(predval) <- pheno$Taxa
grps <- GenerateGroups(ntaxa, fold)
for(i in 1:fold){
toMask <- grps[[i]]
phenoMasked <- pheno
phenoMasked[[2]][toMask] <- NA
mypred <- kin.blup(data = phenoMasked,
geno = "Taxa", pheno = names(pheno)[2],
K = K)
predval[toMask] <- mypred$g[toMask]
}
return(predval)
}
testpred <- PredictPheno(pheno = pheno, K = Msa_A)
plot(pheno$Stem_diameter, testpred)
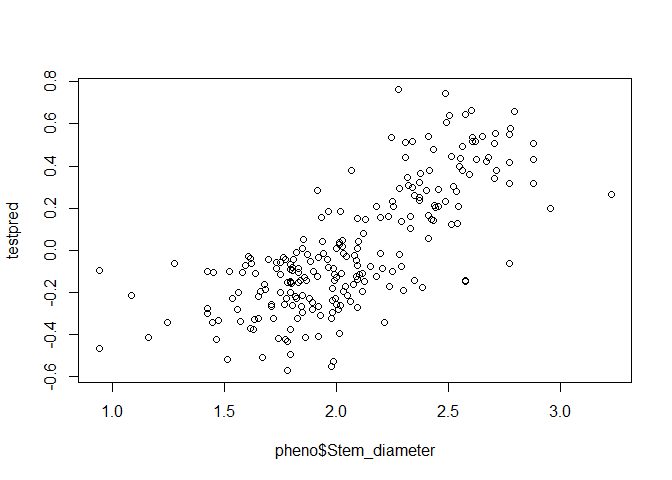
cor(pheno$Stem_diameter, testpred)
## [1] 0.7434333
So on this first test, we have a prediction accuracy of 0.74.
Running replicates of the cross validation
The prediction accuracy could change a lot depending on how individuals are divided into groups. For this reason, we want to repeat the above protocol at least 100 times and see what the average accuracy is.
nreps <- 100
# to hold predicted GEBVs
predmat <- matrix(nrow = nrow(pheno), ncol = nreps,
dimnames = list(pheno$Taxa, NULL))
# to hold prediction accuracy
predacc <- numeric(nreps)
for(i in 1:nreps){
predmat[,i] <- PredictPheno(pheno = pheno, K = Msa_A)
predacc[i] <- cor(pheno$Stem_diameter, predmat[,i])
}
mean(predacc)
## [1] 0.7418571
hist(predacc)
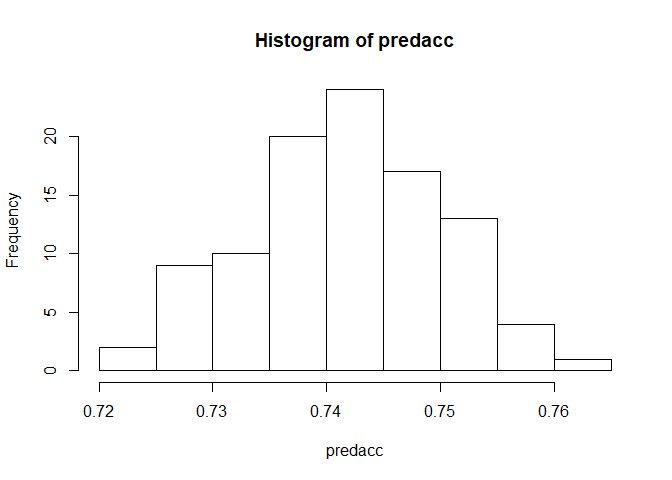
So, 0.74 is the mean prediction accuracy, and it doesn’t tend to very a lot from there.
How can we have an accuracy so high when we only used one chromosome? Most of it can be attributed to the trait being correlated with population structure and relatedness.
If we wanted to export the GEBVs for the purpose of selecting parents for breeding, we could do it like so:
gebvs <- rowMeans(predmat)
gebvs[1:15]
## PMS-458 KMS-widespread UI10-00117 UI11-00005 UI11-00027
## -0.117238229 -0.162218797 0.267862042 0.187367758 0.510918504
## IGR-2011-005 JY186 JY192 JY182 JY009
## 0.599161071 -0.080444245 -0.190773744 -0.050266290 0.194734550
## KMS408 JY008 JY127 KMS417 JY006
## -0.110826811 0.259864597 -0.007564962 -0.040222353 0.385877800
write.csv(gebvs, file = "Msa_gebvs.csv")