Packages for this tutorial
If you don’t have VariantAnnotation, polyRAD, qqman, and pcaMethods installed on your computer already, get them by running the following code:
install.packages("BiocManager")
BiocManager::install("VariantAnnotation")
BiocManager::install("pcaMethods")
install.packages("polyRAD")
install.packages("qqman")
Now load them into your workspace by running:
library(VariantAnnotation)
library(polyRAD)
library(qqman)
library(pcaMethods)
Compressing and inspecting a VCF
PolyRAD takes advantage of the tools available for working with VCF files from the Bioconductor package VariantAnnotation. It is easiest to use those tools if the VCF is compressed using bgzip and indexed. This only needs to be done once, and then the files are saved on your computer.
my_vcf_file <- "three_chs_swetpotato.vcf"
my_vcf_bg <- bgzip(my_vcf_file)
indexTabix(my_vcf_bg, format = "vcf")
We can read the file header to get an idea of what data are in the file.
my_header <- scanVcfHeader(my_vcf_bg)
my_header
## class: VCFHeader
## samples(263): P1_1 P1_2 ... Ind_249 Ind_250
## meta(1): fileformat
## fixed(0):
## info(3): NS DP AF
## geno(5): GT AD DP GQ PL
samples(my_header)[1:50]
## [1] "P1_1" "P1_2" "P1_3" "P1_4" "P1_5" "P1_6" "P1_7"
## [8] "P2_1" "P2_2" "P2_3" "P2_4" "P2_5" "P2_6" "Ind_1"
## [15] "Ind_2" "Ind_3" "Ind_4" "Ind_5" "Ind_6" "Ind_7" "Ind_8"
## [22] "Ind_9" "Ind_10" "Ind_11" "Ind_12" "Ind_13" "Ind_14" "Ind_15"
## [29] "Ind_16" "Ind_17" "Ind_18" "Ind_19" "Ind_20" "Ind_21" "Ind_22"
## [36] "Ind_23" "Ind_24" "Ind_25" "Ind_26" "Ind_27" "Ind_28" "Ind_29"
## [43] "Ind_30" "Ind_31" "Ind_32" "Ind_33" "Ind_34" "Ind_35" "Ind_36"
## [50] "Ind_37"
info(my_header)
## DataFrame with 3 rows and 3 columns
## Number Type Description
## <character> <character> <character>
## NS 1 Integer Number of Samples With Data
## DP 1 Integer Total Depth
## AF . Float Allele Frequency
geno(my_header)
## DataFrame with 5 rows and 3 columns
## Number Type
## <character> <character>
## GT 1 String
## AD . Integer
## DP 1 Integer
## GQ 1 Float
## PL 3 Float
## Description
## <character>
## GT Genotype
## AD Allelic depths for the reference and alternate alleles in the order listed
## DP Read Depth (only filtered reads used for calling)
## GQ Genotype Quality
## PL Normalized, Phred-scaled likelihoods for AA,AB,BB genotypes where A=ref and B=alt; not applicable if site is not biallelic
Importing the VCF into polyRAD
Now we’ll read the VCF into polyRAD. We’ll change a few parameters from their defaults. min.ind.with.reads and min.ind.with.minor.allele are used for filtering and should take the population size and design into account. We have 263 samples, so if we want a maximum of 10% missing data (fairly stringent for GBS datasets) we will set min.ind.with.reads = 237. Since this is an F1 population, any real allele should be found in ~50% of individuals. Let’s relax that to 30% and set min.ind.with.minor.allele = 71. We will also set possiblePloidies = list(6) since we want to treat everything as autohexaploid. Since this is a small example dataset and we know there are only 6000 SNPs, we can also save computer memory by reducing expectedAlleles and expectedLoci.
my_RAD <- VCF2RADdata(my_vcf_bg, min.ind.with.reads = 237,
min.ind.with.minor.allele = 71,
possiblePloidies = list(6),
expectedAlleles = 12000, expectedLoci = 6000)
## Reading file...
## Unpacking data from VCF...
## Filtering markers...
## Phasing 1684 SNPs on chromosome 12
## Phasing 838 SNPs on chromosome 15
## Phasing 1654 SNPs on chromosome 9
## Reading file...
## Unpacking data from VCF...
## Filtering markers...
## Phasing 837 SNPs on chromosome 15
## Reading file...
## 4165 loci imported.
## Building RADdata object...
## Merging rare haplotypes...
## 4107 markers retained out of 4165 originally.
my_RAD
## ## RADdata object ##
## 263 taxa and 4107 loci
## 161558659 total reads
## Assumed sample cross-contamination rate of 0.001
##
## Possible ploidies:
## Autohexaploid (6)
About 1000 SNPs did not pass the filtering criteria, then another ~850 were close enough to each other to be merged into haplotypes. Lastly, ~60 were dropped because no individual allele was common enough to pass the filtering threshold.
Inspecting the RADdata object
We can take a look at the alignment information for our markers.
my_RAD$locTable[1:20,]
## Chr Pos
## Swp_12_0001 12 3924
## Swp_12_0004 12 30530
## Swp_12_0005 12 91124
## Swp_12_0006 12 94713
## Swp_12_0007 12 133529
## Swp_12_0008 12 145679
## Swp_12_0009 12 146201
## Swp_12_0010 12 192541
## Swp_12_0011 12 201994
## Swp_12_0012 12 203147
## Swp_12_0013 12 220259
## Swp_12_0014 12 240553
## Swp_12_0015 12 242030
## Swp_12_0016 12 243515
## Swp_12_0017 12 247758
## Swp_12_0018 12 256965
## Swp_12_0020 12 256998
## Swp_12_0021 12 258052
## Swp_12_0022 12 260765
## Swp_12_0023 12 270995
We can also inspect allele names, and see some markers where SNPs were grouped into haplotypes.
GetAlleleNames(my_RAD)[1:50]
## [1] "Swp_12_0001_TTA" "Swp_12_0001_ACG" "Swp_12_0004_A"
## [4] "Swp_12_0004_T" "Swp_12_0005_T" "Swp_12_0005_A"
## [7] "Swp_12_0006_T" "Swp_12_0006_-" "Swp_12_0007_A"
## [10] "Swp_12_0007_T" "Swp_12_0008_T" "Swp_12_0008_A"
## [13] "Swp_12_0009_A" "Swp_12_0009_T" "Swp_12_0010_A"
## [16] "Swp_12_0010_-" "Swp_12_0011_A" "Swp_12_0011_-"
## [19] "Swp_12_0012_A" "Swp_12_0012_T" "Swp_12_0013_T"
## [22] "Swp_12_0013_C" "Swp_12_0014_A" "Swp_12_0014_G"
## [25] "Swp_12_0015_T" "Swp_12_0015_-" "Swp_12_0016_G"
## [28] "Swp_12_0016_A" "Swp_12_0017_A" "Swp_12_0017_T"
## [31] "Swp_12_0018_AG" "Swp_12_0018_AA" "Swp_12_0018_-G"
## [34] "Swp_12_0020_G" "Swp_12_0020_-" "Swp_12_0021_T"
## [37] "Swp_12_0021_A" "Swp_12_0022_G" "Swp_12_0022_T"
## [40] "Swp_12_0023_A" "Swp_12_0023_T" "Swp_12_0024_C"
## [43] "Swp_12_0024_-" "Swp_12_0025_C" "Swp_12_0025_G"
## [46] "Swp_12_0026_A" "Swp_12_0026_G" "Swp_12_0028_CA"
## [49] "Swp_12_0028_CG" "Swp_12_0028_-A"
Now we see why markers Swp_12_0002 and 3 are missing; they were merged into Swp_12_0001.
Let’s get a quick PCA plot based on allelic read depth, before we do any genotype calling. This will let us confirm that the duplicate parents are really duplicates, and that all the progeny appear to be F1s. First we’ll make a vector of colors to label parents and progeny.
my_col <- rep("black", nTaxa(my_RAD))
names(my_col) <- GetTaxa(my_RAD)
my_col[grep("^P1", GetTaxa(my_RAD))] <- "blue"
my_col[grep("^P2", GetTaxa(my_RAD))] <- "red"
my_col[1:30]
## P1_1 P1_2 P1_3 P1_4 P1_5 P1_6 P1_7 P2_1 P2_2
## "blue" "blue" "blue" "blue" "blue" "blue" "blue" "red" "red"
## P2_3 P2_4 P2_5 P2_6 Ind_1 Ind_2 Ind_3 Ind_4 Ind_5
## "red" "red" "red" "red" "black" "black" "black" "black" "black"
## Ind_6 Ind_7 Ind_8 Ind_9 Ind_10 Ind_11 Ind_12 Ind_13 Ind_14
## "black" "black" "black" "black" "black" "black" "black" "black" "black"
## Ind_15 Ind_16 Ind_17
## "black" "black" "black"
Then we can make the plot.
plot(my_RAD, col = my_col)
## Performing principal components analysis...
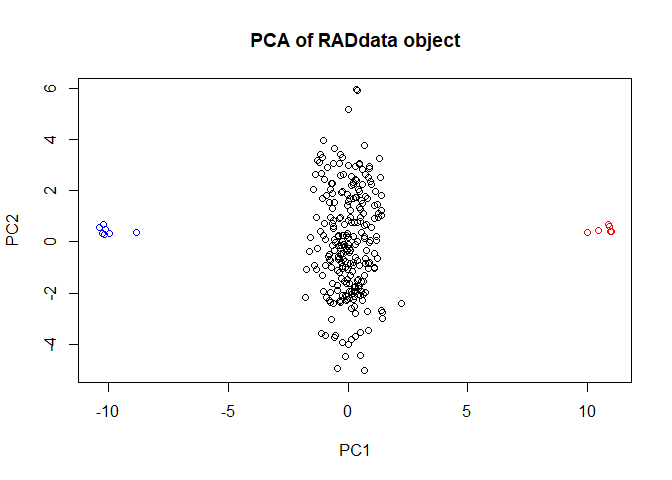
This looks perfect. We don’t need to remove any samples. (If we did, the SubsetByTaxon function would be helpful.) We can also merge read depth across parental duplicates.
my_RAD <- MergeTaxaDepth(my_RAD, paste("P1", 1:7, sep = "_"))
## 7 taxa will be merged into the taxon P1_1.
my_RAD <- MergeTaxaDepth(my_RAD, paste("P2", 1:6, sep = "_"))
## 6 taxa will be merged into the taxon P2_1.
GetTaxa(my_RAD)[1:20]
## [1] "P1_1" "P2_1" "Ind_1" "Ind_2" "Ind_3" "Ind_4" "Ind_5"
## [8] "Ind_6" "Ind_7" "Ind_8" "Ind_9" "Ind_10" "Ind_11" "Ind_12"
## [15] "Ind_13" "Ind_14" "Ind_15" "Ind_16" "Ind_17" "Ind_18"
For genotype calling, we will need to indicate which samples are the parents. Since there was no backcrossing, it does not matter which is listed as “donor” and which as “recurrent”.
my_RAD <- SetDonorParent(my_RAD, "P1_1")
my_RAD <- SetRecurrentParent(my_RAD, "P2_1")
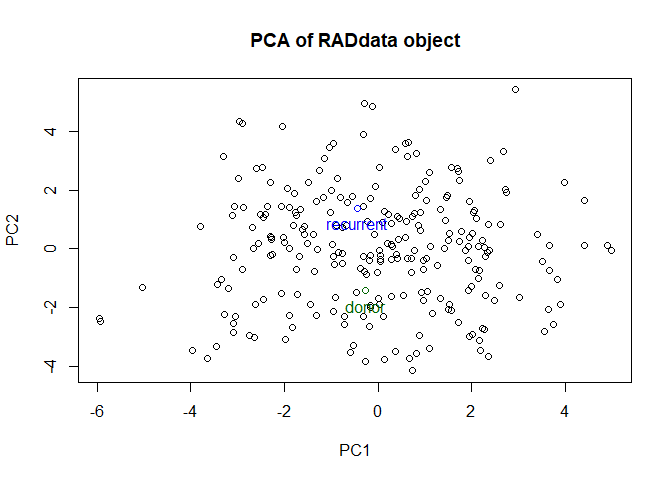
We can do another quick PCA to see how it looks now. Since there is only one sample of each parent, the first axis no longer distinguishes parents and progeny.
plot(my_RAD)
## Performing principal components analysis...
Testing overdispersion
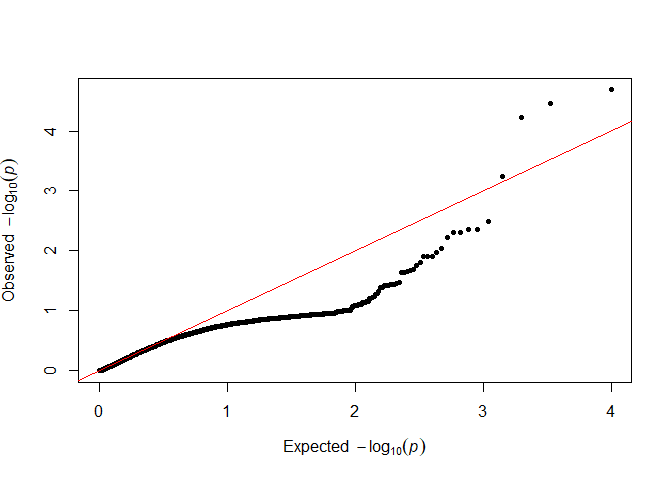
Because sequencing data are noisy, read depth ratios might deviate from the underlying allele dosage ratios more than we would expect. We can perform preliminary genotype calling, then test for this overdispersion. (I’m using sample to reduce the amount of time it takes to generate the plot, by only using a random subset of p-values.)
my_RAD_pre <- PipelineMapping2Parents(my_RAD, freqAllowedDeviation = 0.035,
useLinkage = FALSE)
## Making initial parameter estimates...
## Done.
testOD <- TestOverdispersion(my_RAD_pre)
qq(sample(testOD[["10"]], 5000))
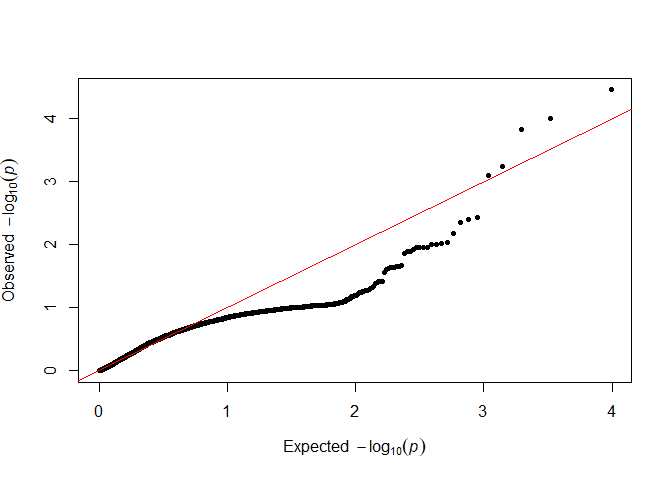
qq(sample(testOD[["12"]], 5000))
qq(sample(testOD[["14"]], 5000))
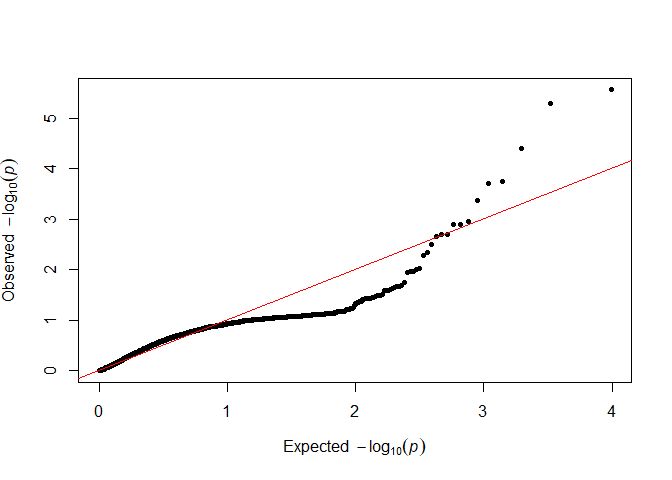
We want as many points as possible to follow the red line in the lower left, so we will go forward with 12 as our value.
Genotype calling
We will perform genotype calling using expected genotype frequencies in an F1 population as priors. This time, we will adjust our overdispersion parameter, and also add linkage to the model.
my_RAD <- PipelineMapping2Parents(my_RAD, freqAllowedDeviation = 0.035,
useLinkage = TRUE, overdispersion = 12)
## Making initial parameter estimates...
## Updating priors using linkage...
## Done.
If polyRAD was not able to determine the inheritance pattern, the posterior probabilities will be filled with NAs. Additionally, if both parents were scored as homozygous, the progeny will be non-variable and the marker will not be particularly useful. We can identify and remove such markers.
my_RAD_sub <- RemoveUngenotypedLoci(my_RAD,
removeNonvariant = TRUE)
my_RAD_sub
## ## RADdata object ##
## 252 taxa and 2347 loci
## 99739604 total reads
## Assumed sample cross-contamination rate of 0.001
##
## Possible ploidies:
## Autohexaploid (6)
##
## Allele frequencies estimated for mapping
Here we retain 2347 loci. We will use that subset for further analysis.
Genotype export
We can produce a matrix of the most probable genotypes.
out_geno <- GetProbableGenotypes(my_RAD_sub, naIfZeroReads = TRUE)$genotypes
out_geno[1:20,1:7]
## Swp_12_0001_ACG Swp_12_0004_T Swp_12_0005_A Swp_12_0007_T
## P1_1 3 0 0 1
## P2_1 1 1 1 1
## Ind_1 2 1 1 1
## Ind_2 2 1 1 1
## Ind_3 3 1 1 1
## Ind_4 1 1 1 1
## Ind_5 2 1 1 1
## Ind_6 2 1 1 1
## Ind_7 3 1 1 1
## Ind_8 3 1 1 1
## Ind_9 2 1 1 1
## Ind_10 2 1 1 1
## Ind_11 2 1 1 1
## Ind_12 2 1 1 1
## Ind_13 2 1 1 1
## Ind_14 2 1 1 1
## Ind_15 3 1 1 1
## Ind_16 1 1 1 1
## Ind_17 2 1 1 1
## Ind_18 2 1 1 1
## Swp_12_0008_A Swp_12_0009_T Swp_12_0011_-
## P1_1 0 0 0
## P2_1 1 1 1
## Ind_1 1 1 1
## Ind_2 1 1 1
## Ind_3 1 1 1
## Ind_4 1 1 1
## Ind_5 1 1 1
## Ind_6 1 0 1
## Ind_7 1 0 1
## Ind_8 1 1 1
## Ind_9 1 1 1
## Ind_10 1 0 1
## Ind_11 1 1 1
## Ind_12 1 0 1
## Ind_13 1 0 1
## Ind_14 1 0 1
## Ind_15 1 1 1
## Ind_16 1 1 1
## Ind_17 1 1 1
## Ind_18 1 1 1
A PCA can confirm that the relatedness among individuals still looks right.
my_pca <- pca(out_geno, method = "ppca")
plot(scores(my_pca)[,1], scores(my_pca)[,2],
col = c("blue", "red", rep("black", nrow(out_geno) - 2)))
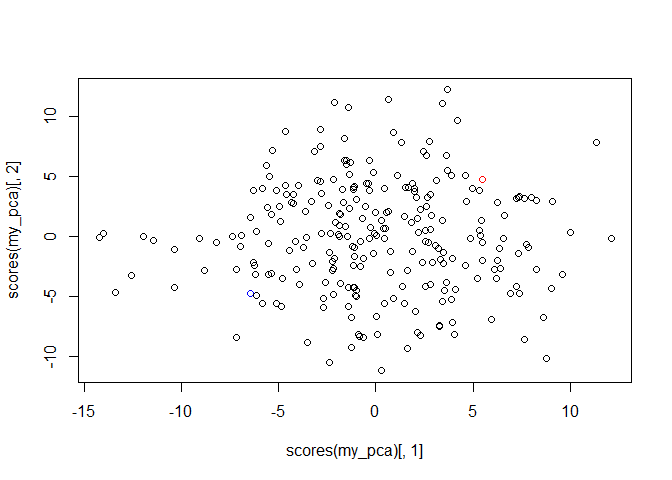
Now that genotypes have been called, we see progeny as being mostly between the two parents on the first axis.
We can also see the posterior mean genotypes
out_postmean <- GetWeightedMeanGenotypes(my_RAD_sub, minval = 0, maxval = 6)
out_postmean[1:20, 1:7]
## Swp_12_0001_ACG Swp_12_0004_T Swp_12_0005_A Swp_12_0007_T
## P1_1 3.2046918 1.0254678 1.1151566 1.039102
## P2_1 1.3644259 1.0706542 1.2166453 1.043754
## Ind_1 2.1474927 0.9998886 0.9999984 1.000004
## Ind_2 2.0758444 0.9999844 0.9999997 1.000368
## Ind_3 2.4959398 0.9998597 0.9999980 1.000002
## Ind_4 1.5564783 0.9997394 0.9999931 1.000002
## Ind_5 2.2979795 0.9999889 0.9999998 1.002052
## Ind_6 2.0396853 0.9997983 0.9999993 1.000001
## Ind_7 2.5439993 0.9998733 0.9999972 1.000004
## Ind_8 2.5786597 0.9995354 0.9999977 1.000002
## Ind_9 1.9908908 0.9999536 0.9999991 1.000004
## Ind_10 2.1113531 0.9991366 0.9999933 1.000000
## Ind_11 1.7515587 0.9997548 0.9999975 1.000001
## Ind_12 1.6892979 0.9999581 0.9999994 1.000018
## Ind_13 2.2979795 0.9993534 0.9999952 1.000000
## Ind_14 1.9979533 0.9994706 0.9999975 1.000001
## Ind_15 2.6422610 0.9999832 0.9999992 1.000198
## Ind_16 0.6923537 0.9998979 0.9999991 1.000024
## Ind_17 1.8786148 0.9999149 0.9999996 1.000003
## Ind_18 1.9593875 0.9998810 0.9999995 1.000007
## Swp_12_0008_A Swp_12_0009_T Swp_12_0011_-
## P1_1 1.091852 1.05608013 1.0786582
## P2_1 1.184044 1.17331927 1.2021079
## Ind_1 1.000000 0.99861175 1.0000000
## Ind_2 1.000000 0.99963611 1.0000000
## Ind_3 1.000000 0.98472802 1.0000000
## Ind_4 1.000000 0.99840325 0.9999999
## Ind_5 1.000000 0.99827699 1.0000000
## Ind_6 1.000000 0.07645925 1.0000000
## Ind_7 1.000000 0.06019943 1.0000000
## Ind_8 1.000000 0.99493510 1.0000000
## Ind_9 1.000000 0.99923369 0.9999999
## Ind_10 1.000000 0.19253141 0.9999999
## Ind_11 1.000000 0.99822221 1.0000000
## Ind_12 1.000000 0.20776835 1.0000000
## Ind_13 1.000000 0.31445458 0.9999991
## Ind_14 1.000000 0.17879608 0.9999999
## Ind_15 1.000000 0.99412682 1.0000000
## Ind_16 1.000000 0.99942423 1.0000000
## Ind_17 1.000000 0.99968061 1.0000000
## Ind_18 1.000000 0.99876567 1.0000000
Some of these don’t match the expected segregation ratio, and upon inspection of read depths, we see that the depth ratios don’t meet expectations for a hexaploid.
my_RAD_sub$alleleDepth[1:20,9:14]
## Swp_12_0008_T Swp_12_0008_A Swp_12_0009_A Swp_12_0009_T
## P1_1 1179 105 38 1
## P2_1 1006 131 130 15
## Ind_1 277 39 7 1
## Ind_2 92 23 5 2
## Ind_3 226 18 48 1
## Ind_4 180 17 22 2
## Ind_5 226 34 9 1
## Ind_6 210 14 26 0
## Ind_7 170 12 31 0
## Ind_8 252 12 23 1
## Ind_9 227 14 12 2
## Ind_10 149 21 11 0
## Ind_11 160 12 38 3
## Ind_12 116 15 10 0
## Ind_13 234 15 5 0
## Ind_14 206 10 12 0
## Ind_15 213 22 52 2
## Ind_16 161 16 9 2
## Ind_17 197 13 16 4
## Ind_18 127 15 6 1
## Swp_12_0011_A Swp_12_0011_-
## P1_1 1684 139
## P2_1 1177 162
## Ind_1 392 31
## Ind_2 262 42
## Ind_3 278 33
## Ind_4 295 12
## Ind_5 194 27
## Ind_6 327 17
## Ind_7 572 41
## Ind_8 426 24
## Ind_9 173 7
## Ind_10 437 20
## Ind_11 279 18
## Ind_12 363 36
## Ind_13 324 6
## Ind_14 173 7
## Ind_15 311 22
## Ind_16 265 34
## Ind_17 224 19
## Ind_18 392 34
We can save the RADdata object, and also export to MAPpoly.
save(my_RAD_sub, file = "sweetpotato_F1_RADdata.RData")
Export_MAPpoly(my_RAD_sub, file = "sweetpotato_F1_polyRAD_MAPpoly.txt")
Comparison to SuperMASSA results
load("supermassa_result.rda")
dat.swp$geno.dose[1:10,1:10]
## Ind_1 Ind_10 Ind_100 Ind_101 Ind_102 Ind_103 Ind_104 Ind_105
## Swp_12_0005 7 7 7 7 7 7 7 7
## Swp_12_0006 7 3 2 7 2 7 7 7
## Swp_12_0008 7 7 7 7 7 7 7 7
## Swp_12_0009 7 0 0 7 1 7 0 7
## Swp_12_0010 7 3 7 7 2 7 7 4
## Swp_12_0011 7 7 7 7 7 7 7 7
## Swp_12_0013 7 7 7 7 7 7 7 7
## Swp_12_0014 7 7 7 7 7 7 7 7
## Swp_12_0015 0 7 0 0 0 0 0 7
## Swp_12_0017 7 7 7 7 7 7 7 7
## Ind_106 Ind_107
## Swp_12_0005 7 7
## Swp_12_0006 7 7
## Swp_12_0008 7 7
## Swp_12_0009 0 0
## Swp_12_0010 7 3
## Swp_12_0011 7 7
## Swp_12_0013 7 7
## Swp_12_0014 7 7
## Swp_12_0015 0 0
## Swp_12_0017 7 7
We’ll calculate the posterior mean genotypes from the SuperMASSA results to compare to those from polyRAD.
prob_supermassa <- as.matrix(dat.swp$geno[,-(1:2)])
wm_vect <- rowSums(sweep(prob_supermassa, 2, 0:6, "*"))
postmean_supermassa <- matrix(0, nrow = dat.swp$n.ind, ncol = dat.swp$n.mrk,
dimnames = list(dat.swp$ind.names, dat.swp$mrk.names))
for(i in 1:nrow(dat.swp$geno)){
ind <- dat.swp$geno$ind[i]
mrk <- dat.swp$geno$mrk[i]
postmean_supermassa[ind, mrk] <- wm_vect[i]
}
We’ll get correlations between posterior mean genotypes from SuperMASSA and posterior mean genotypes from polyRAD.
common_loc <- GetLoci(my_RAD_sub)[GetLoci(my_RAD_sub) %in% dat.swp$mrk.names]
my_corr <- rep(NA_real_, length(common_loc))
names(my_corr) <- common_loc
for(mrk in common_loc){
polyRAD_match <- grep(mrk, colnames(out_postmean))
if(length(polyRAD_match) > 1) next
geno1 <- postmean_supermassa[,mrk]
geno2 <- out_postmean[dat.swp$ind.names, polyRAD_match]
my_corr[mrk] <- cor(geno1, geno2, use = "pairwise.complete.obs")
}
hist(my_corr)
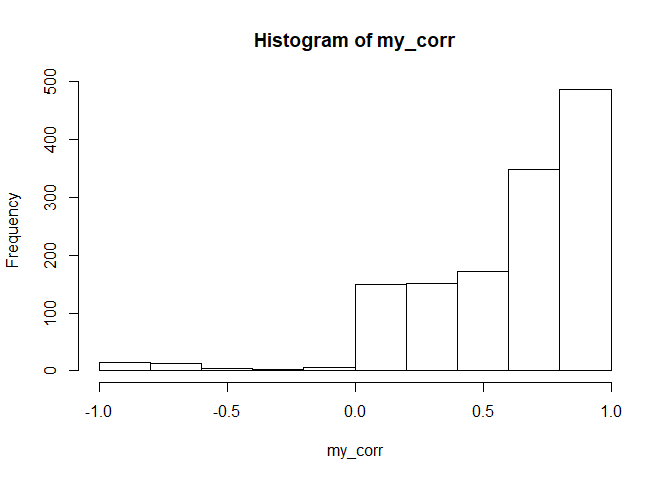
median(my_corr, na.rm = TRUE)
## [1] 0.7167871
Most, but not all, markers have moderately high correlation between the two methods.